CityU scientists classify knots efficiently with artificial intelligence
AlphaGo, the artificial intelligence programme that plays chess, has made history by defeating two human world champions from China and South Korea. AlphaGo’s impressive victory over the sophisticated human brains is considered one giant step for artificial intelligence. Its “intelligence” is built from neural networks, a machine learning technology. Recently, scientists from City University of Hong Kong (CityU) and his collaborators have trained artificial neural networks to classify knots, achieving an accuracy of over 99%. It proves that machine learning can facilitate knot research in mathematical and physical sciences.
Their research findings were published in the scientific journal Physical Review E, titled “Identifying knot types of polymer conformations by machine learning”. Moreover, it was later featured in the “Research Highlights” section of the prestigious scientific journal Nature.
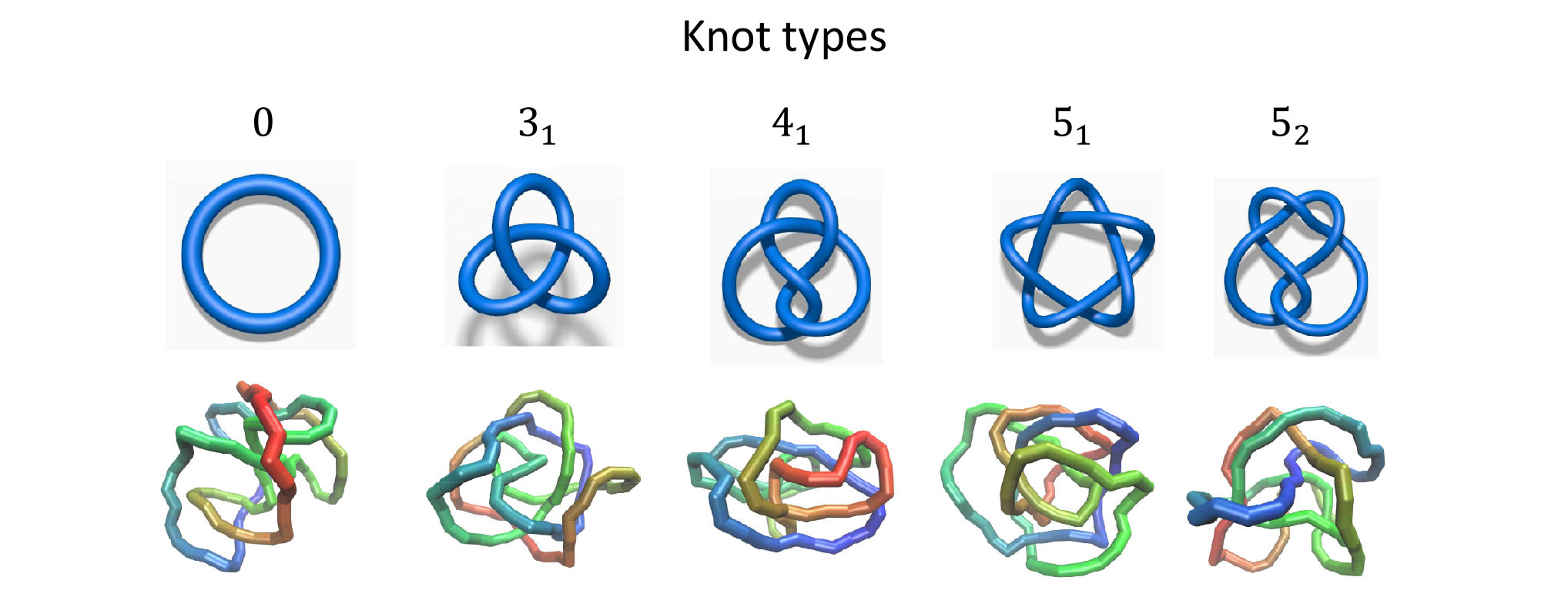
Knots commonly found in different fields in science
Scientists in different fields are interested in different properties of “knots”. For example, some biophysicists have discovered that the “knots” can tighten protein structures to facilitate some special biocatalytic functions. “Knots” in DNA can impede replication, transcription, and cell divisions, and hence some enzymes called topoisomerases are developed to untie “knots” in vivo. Also, “knots” in DNA can slow down the translocation speed through a nanopore, which may facilitate the development of nanopore sequencing technology.
For mathematicians studying knot theory, “knot” here refers to a topological property in a string with closed ends. The knot remains the same no matter how the string deforms.
Knot identification: an unsolved problem in mathematical and physical sciences
For decades, mathematicians are puzzled about how to determine whether any two knots are of the same type: whether the knots can be converted into each other without cutting the string. So far, no practical method exists to classify all knots. For simpler knots, mathematicians developed some algorithms to classify them. However, calculation by these algorithms is inefficient, and the computational time grows exponentially with the knot complexity.
Nowadays, artificial intelligence is catching up with the human brain through machine learning. It outperforms humans in image recognition and even playing chess. Then can machine learning be used to solve other kinds of problems? With this question in mind, Dr Dai Liang, Assistant Professor from CityU’s Department of Physics who led the research, tested the ability of artificial neural networks in solving the knot identification problem. “Knot classification is an important and unsolved problem in mathematical and physical sciences, and neural networks may provide new insights into this problem,” said Dr Dai.
Neural networks are “taught” to identify knots
So how do artificial intelligence systems learn?
They can be trained via a data-processing task and learn from it by adjusting to the feedback signal during training. One way of training is deep learning, meaning that a large number of disordered signals are sorted out into useful information through layered processing, and then solve the problems. Those layered data-encoding models are artificial neural networks. “They simulate the connected networks of neurons in human brains. ‘AlphaGo’, the artificial intelligence programme developed by Google also uses such technology,” explained Dr Dai.
Dr Dai’s team first generated millions of samples of the five chosen knot types by computer simulation. Those knots are usually too complicated to be identified visually. The team also designed two types of neural network models, namely feed-forward neural network and recurrent neural network. These two models were then trained to classify the knot samples mentioned above.
Leveraging on the bidirectional processing pattern of recurrent neural network
“Using neural network models to classify knots is 20 times faster than calculating with conventional algorithms. Moreover, neural network models have learnt to predict knot types on unseen samples,” said Dr Dai. Researchers applied the trained models to identify one million unseen knots. The feed-forward network can predict with an accuracy of around 70%, while the recurrent neural network model performed even better, with a prediction accuracy of over 99%.
Researchers believed that the impressive performance of the recurrent neural network can be attributed to its “bidirectional processing pattern” of different layers. Inputs will be sent forward and backward between and within different processing layers. This kind of context-awareness enables the sequence information to be used more efficiently. Furthermore, the team used a refined formulation of the recurrent neural network called long short-term memory, which would screen useless information to improve predictive power. Also, researchers found that prediction accuracy improves with a larger training sample size.
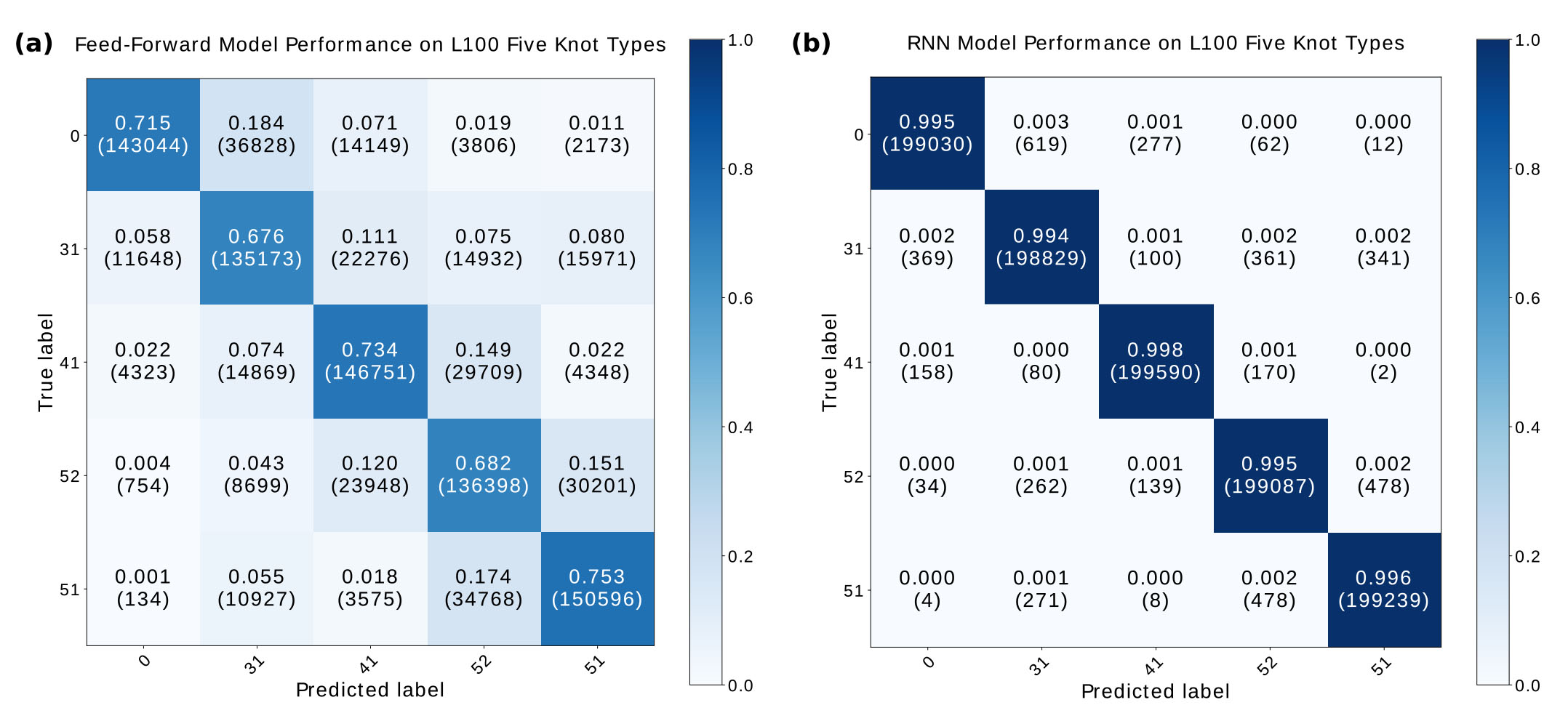
“Our research has proved that neural networks can be an efficient tool to tackle knot classification, which is a special and difficult problem. Neural networks can recognize the patterns of knots and achieve remarkable success rates in knot classification. We hope artificial intelligence can provide new insights and tools to solve important problems in mathematics and physical sciences, which are hard to be tackled by traditional approaches.” concluded Dr Dai.
Dr Dai is the corresponding author of the paper. Co-first authors of the paper are Olafs Vandans, a research assistant from CityU’s Department of Physics, and Yang Kaiyuan, a research assistant from National University of Singapore. Professor Wu Zhongtao, Associate Professor from The Chinese University of Hong Kong’s Department of Mathematics, is also the co-author of this paper.

The study was supported by CityU, Hong Kong Research Grants Council, Guangdong Basic and Applied Basic Research Fund, and National Natural Science Foundation of China.
DOI number: 10.1103/PhysRevE.101.022502
