Working Examples
Here, the use of our programs is demonstrated:
Firstly, we create three ideals signals, namely y, x1 and x2. y comprises of sine waves of period
t=[-100:1:100];
y=sin(t*2*pi)+sin(t*2*pi/4)+sin(t*2*pi/8)+sin(t*2*pi/16)+sin(t*2*pi/32)+sin(t*2*pi/64);
x1=sin(t*2*pi/4);
x2=sin(t*2*pi/16);
|
The
corresponding wavelet power spectrum can be plotted using Aslak
Grinsted's Matlab function inside the combined software package (you should have
this function ready when combining our software package with that of
Aslak Grinsted, see Download page):
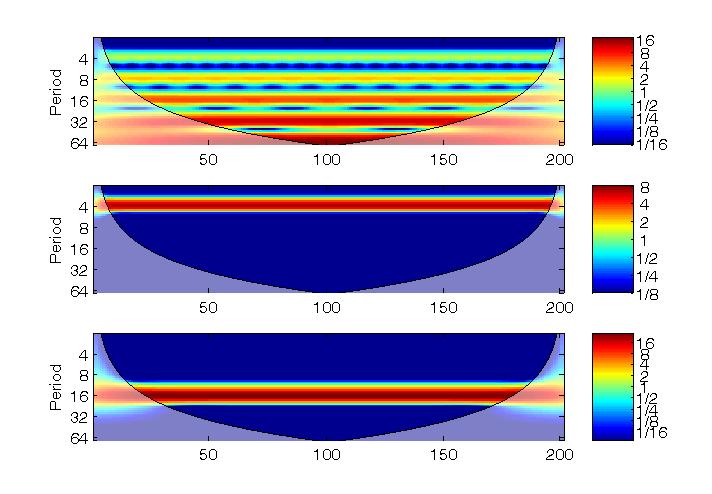 |
subplot(3,1,1);
wt(y);
subplot(3,1,2);
wt(x1);
subplot(3,13);
wt(x2); |
Partial wavelet coherence
The partial wavelet conherence squared on y and x1 to reveal their stand-alone relationship (after the removal of the influence of x2):
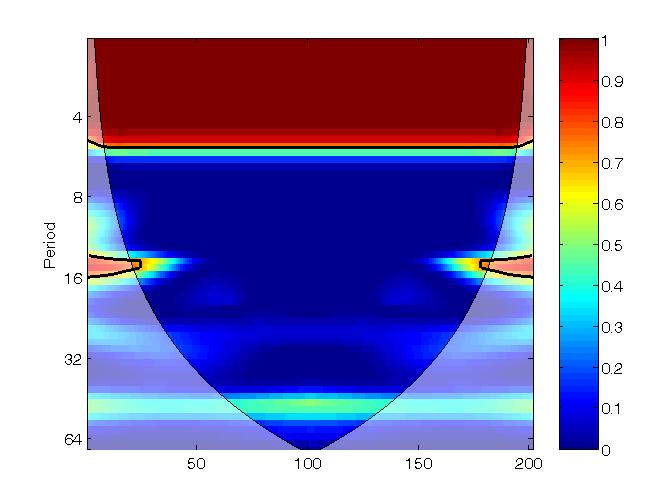 |
pwc(y, x1, x2); |
Multiple wavelet coherence
The multiple wavelet coherence squared of y, x2 and x1, which gives the resulting wavelet coherence squred that computes the proportional of wavelet power of the y explained by x2 and x1:
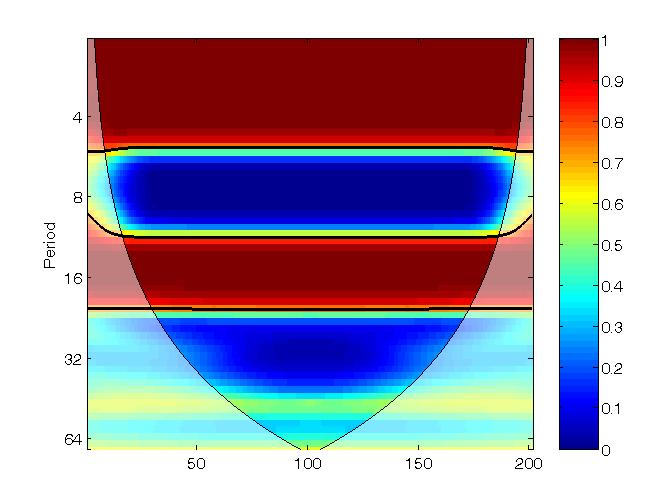 |
mwc(y, x2, x1); |
Rectified wavelet power specturm
The bias problem of wavelet power spectrum found in previous software packages (top) is rectified (bottom) according to
Liu et al. (2007):
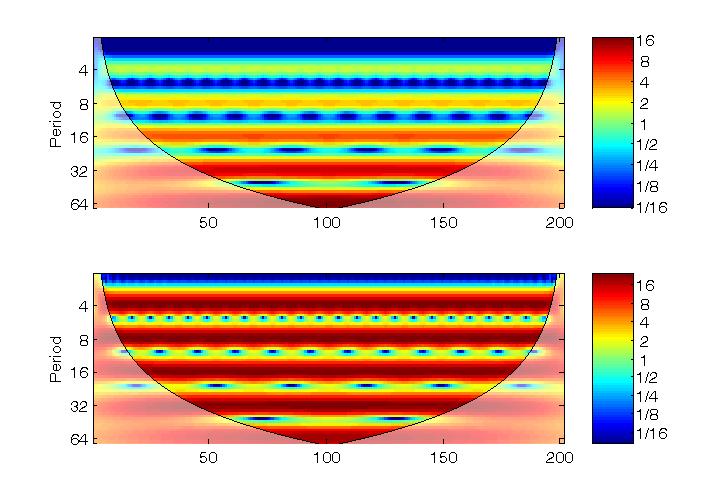 |
subplot(2,1,1);
wt(y);
subplot(2,1,2);
wtrec(y); |
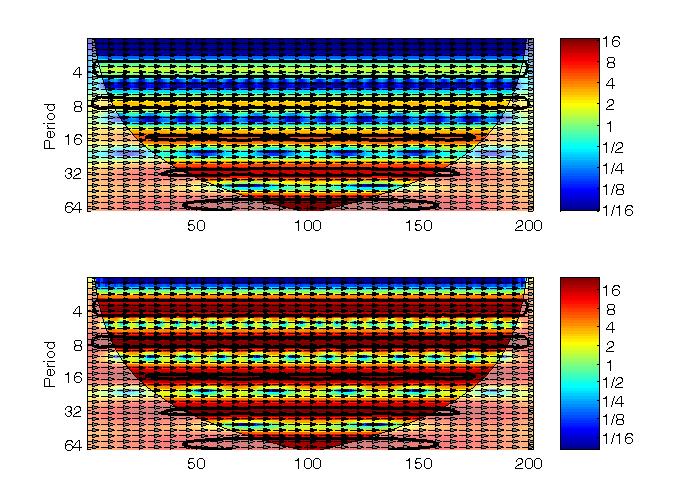
Rectified wavelet cross specturm
The bias problem of wavelet power spectrum found in previous software
packages (top) is rectified (bottom) according to
Veleda et al. (2012):
 |
subplot(2,1,1);
xwt(y,y);
subplot(2,1,2);
xwtrec(y,y); |
Should you have any enquiry, please feel free to contact:
Eric K. W. Ng
Email:
E.Ng@cityu.edu.hk




